|
INTRODUCCIÓN Contenido (1). En el trabajo se utiliza el término médico para hacer referencia a las personas que poseen por lo menos el título de médico cirujano, el grado médico básico en México. La técnica analítica básica es el análisis de regresión múltiple; primero, para explorar relaciones entre las medidas de demanda disponibles y los índices de desarrollo económico y social, y segundo, para desarrollar ecuaciones con qué proyectar la demanda entre 1965 Y 1980. El análisis es de tipo transversal y se utilizan como unidades de observación las 32 entidades federativas de México e información de dos años base o puntos de equilibrio : 1960 Y 1965.
I. PROBLEMAS DE INFORMACION Y METODO Contenido Las fuentes básicas de los datos comprenden las proyecciones de población del Banco de México,(2) el censo de población de 1960 y las recopilaciones intercensales de 1965. Las proyecciones demográficas se basan en los totales revisados del censo de 1960 y en supuestos altos, bajos e intermedios, respecto a cambios en las tasas de fecundidad. Las proyecciones intermedias son las más detalladas y abarcan (con ajustes respecto a la esperanza de vida y la migración interna) incrementos de población por sexo, grupos de edad, estado y territorio, y la residencia rural y urbana, en 1965, 1970, 1975 Y 1980. Estas proyecciones intermedias son las que se utilizan, sin alteración, en el presente trabajo. (2). Raúl Benítez Zenteno y Gustavo Cabrera Acevedo, Proyecciones de la población de México, 1960-1980, México, Banco de México, Departamento de Investigaciones Industriales, 1966. La información correspondiente a la demanda de médicos y el desarrollo económico y social es menos completa. En el cuadro 1 se señala la información disponible (o elaborada) de 1960 y 1965. Hay algunas inconsistencias y omisiones importantes. En primer lugar, la información sobre 1960 es más completa que la de 1965, lo que significa que la mayoría de las ecuaciones elaboradas con la primera no se pueden comprobar con un segundo conjunto de observaciones. En segundo lugar, la información respecto a médicos no se puede desagregar en trabajo de tiempo parcial o de tiempo completo. En 1960 había 20,590 médicos(3) y 25,062 en 1965.(4) No hay manera de estimar el número de "equivalentes de tiempo completo" que representan estos totales. Es común tener empleos múltiples. Los médicos que trabajan en la administración gubernamental o en proyectos de salud pública durante el día, frecuentemente ejercen la medicina en clínicas privadas por la noche. Para fines de análisis, es necesario suponer que los tiempos parciales representan la misma proporción de la oferta en cada entidad. Un supuesto similar es que todos los tiempos parciales (o la misma proporción) se computaron en cada entidad. (3) Miguel Huerta Maldonado, Manual de geomédica mexicana, México, Instituto Mexicano del Seguro Social, 2a edición, 1966. Este compendio (preparado por y para los planificadores en el campo de la salud dentro del sistema de seguridad social) está basado en tabulaciones especiales del censo de 1960. Los datos se refieren al mes de junio. (4). Ibid. 3a ed. El mismo compendio que se refiere a 1965 está basado en registros de
empleo (por nombre, para evitar un cómputo doble) en las secretarías de Estado, los sistemas de seguridad
social, los hospitales privados, las asociaciones profesionales y las escuelas médicas. La información
se refiere al mes de diciembre. El cómputo inicial no incluyó 29 médicos en el Estado de México
que se habían graduado en la escuela médica del Estado entre 1960 y 1965. En edición posterior
se corregirá este error, suponiendo que todos los graduados permanecieron en el Estado y se hicieron médicos
en ejercicio de la profesión. En todo el trabajo he utilizado los datos revisados, incrementando el total
de médicos en el Estado de 439 a 468, y el total nacional de 25,033 a 25,062. CUADRO 1 MEXICO : INFORMACION DISPONIBLE PARA ANALIZAR LA DEMANDA DE MEDICOS, 1960 Y 1965, POR ESTADOS Y TERRITORIOS
La variable dependiente. Más grave aún, no existen datos sobre el promedio anual de visitas médicas por persona ni sobre el promedio de los gastos médicos anuales por persona. Además, no hay datos sobre la clientela y personal real de la medicina institucional y privada debido a que los diversos servicios de salud gubernamentales se traslapan entre sí (y con la atención privada) en cobertura y en personal. Por lo tanto, las únicas variables dependientes disponibles son los cocientes globales de médicos entre población en cada entidad en 1960 y 1965. Esta limitación es importante ya que las relaciones no distinguen diferencias en la calidad y la productividad de la fuerza de trabajo médica, ni tampoco indican la medida en que el personal disponible es de hecho "demandado" y utilizado.(5) Para efectuar el análisis es necesario suponer que estas relaciones representan dos conjuntos de puntos de equilibrio entre la demanda del gobierno y la privada sumadas y la oferta total. (La validez de este supuesto se examina más adelante.) El objetivo del análisis es determinar el grado en que las variaciones en el número de médicos por 10,000 se asocian con diferencias en los niveles de desarrollo económico y social. (5). Las relaciones tampoco distinguen diferencias en densidad, distancia y transporte, factores que en conjunto afectan el acceso a la atención médica. Véase Gary W. Shannon, Rashid L. Bashur y Charles A. Metzer, "The Concept of Distance as a Factor in Accessibility and Utilization of Health Care", Medical Care Review Vol. 26, Núm. 2, febrero de 1969, pp. 143-161. Sin embargo, en México la proporción de la población que vive en ciudades (de 2,500 y más) probablemente es una buena aproximación a éstas (y otras) diferencias. Análisis transversal. Otro problema se refiere a que el estudio se limita a un análisis transversal que utiliza las 32 entidades como unidades de observación. Se plantea la pregunta de si los resultados serían los mismos si se utilizaran otros conjuntos de datos y otras poblaciones. No hay cifras sobre "áreas de mercado de servicios médicos" ni sobre desagregaciones similares. ¿Es posible que el uso de entidades como unidades de observación sesgue los resultados?, y, si es el caso, ¿en qué dirección? En el cuadro 2 se señalan los cocientes de médicos entre población en cada entidad y en el país en su conjunto en 1960 y 1965. Es obvio que la distribución era (y es) desigual y que empeoró entre 1960 y 1965. De un incremento neto de 4,472 médicos, 2,430 correspondieron al Distrito Federal y 1,049 al estado de Jalisco, en particular a la ciudad de Guadalajara.(6) Por lo tanto, los cocientes de médicos entre población aumentaron en estas regiones pero disminuyeron en tres cuartos de las entidades y regiones restantes, incluida la mayoría de las más pobres. Y en Yucatán, Zacatecas, Hidalgo, Guerrero y Tlaxcala,(7) el número de médicos disminuyó en cifras absolutas. (6). Cálculos a partir de información en Huerta Maldonado, op. cit. y 3ª ed.). (7). Ibid. Sin embargo, es probable que estas relaciones de hecho subestimen la amplitud de las disparidades en los servicios y la demanda de médicos. Primero, las entidades no son unidades homogéneas y en cualquiera de ellas el cociente de médicos entre población es simplemente un promedio de las concentraciones en algunas localidades y de la escasez en otras. Si fuera posible distinguirlas, las diferencias entre las áreas de mercado homogéneas de servicios médicos serían mucho mayores que las diferencias entre entidades. Segundo, la calidad y la naturaleza del personal y de los servicios varía según los niveles de desarrollo y la cobertura de la medicina pública. El ingreso y la demanda son más bajos en las entidades más pobres y una proporción menor de su población recibe servicios de salud. Como resultado, los médicos en estas entidades tienden a ser de edad avanzada, deficientemente entrenados y principalmente dedicados a la práctica privada;(8) atienden pocos pacientes al día, tienen menos equipo y personal y utilizan métodos de diagnóstico y tratamiento que ya no son utilizados por los médicos ni los servicios de salud de las regiones más avanzadas del país.(9) (8). Huerta Maldonado, op. cit. (3ª ed.). (9). Esta generalización -y las cifras del cuadro 2- excluyen alrededor de 1,400 estudiantes
de medicina que hacen servicio social cada año. Se requiere un año de servicio de cada estudiante
de medicina inmediatamente antes de su examen y tesis profesionales. Este programa data de 1936 y se diseñó
para contrarrestar la mala distribución de médicos, a fin de proporcionar personal a las áreas
rurales e inducir a los médicos jóvenes para que ejercieran su profesión en estas regiones
después de graduarse. Sin embargo, en los años recientes, más del 28% de los estudiantes -en
contraste con el 3% en 1946- han efectuado su servicio social en las ciudades, trabajando en los servicios de salud
y regresando a ellos después de su graduación. Véase José Manuel Alvarez Manilla, Proyecto
de programa para el servicio social de los pasantes de medicina de la UNAM, México, Universidad Nacional
Autónoma de México, tesis profesional, Facultad de Medicina, 1962, pp. 36, 55-56. Sólo una
pequeña proporción -en 1960 se estimó el 6%- de los estudiantes que trabajan en las zonas
rurales durante su servicio social regresan a ejercer allí posteriormente. CUADRO 2 MEXICO : COCIENTES DE MEDICOS ENTRE POBLACION, 1960 Y 1965, POR ENTIDADES
Dado que las relaciones calculadas no distinguen diferencias dentro de las entidades, ni diferencias entre entidades en cuanto a calidad y productividad, es inevitable que subestimen diferencias en la distribución de personal y servicios, y por lo tanto en la demanda. Las proyecciones basadas en otras poblaciones (que midieran la demanda por tasa de uso más que por relaciones) indudablemente serían más elevadas. Esta deficiencia no se puede evitar y de cualquier manera la demanda proyectada, aun conteniendo la subestimación, es suficientemente elevada para poner en duda la viabilidad de la política médica actual.
¿Cuáles son entonces los factores que permiten "pronosticar" mejor el número y la distribución de los médicos en México? Prueba del modelo y de las variables. La primera etapa consiste en un análisis de regresión múltiple por mínimos cuadrados, de la información de 1960, basado en la hipótesis de que la distribución (o "demanda") es función de los niveles de urbanización, ingresos, educación y vida, así como de aculturación. Esto se expresa en la siguiente forma : Yi = a + bUi + cGi + dEi + eHi + fPi + gWi + hSi Donde: Y = número de médicos por 10,000 habitantes
Se eligió un modelo de regresión lineal debido a dos razones : por sencillez y por su similitud con el modelo desarrollado por Baker y Perlman en Taiwan.(10) Además, aunque el objetivo de esta etapa inicial del análisis es determinar únicamente el poder de pronóstico de las variables que parecen estar relacionadas con la demanda, se encuentran también presentes las condiciones estadísticas que permiten que se utilice el modelo para estimar los efectos de cada variable por separado : por razones prácticas, las variables independientes son independientes del número de médicos por 10,000 habitantes y, salvo una excepción, la multicolinealidad entre ellas se encuentra dentro de límites tolerables.(11) (10). Timothy D. Baker y Mark Perlman, Health Manpower in a Developing Economy. Baltimore, The Johns Hopkins Press, 1967, pp. 139-144. (11). Una alta covarianza, y/o la inclusión de una variable endógena, entre las variables independientes (o exógenas) introduce "un sesgo en la estimación estadística de los parámetros" de un modelo de regresión por mínimos cuadrados. Sin embargo, éste no es un problema si el objetivo es pronosticar los valores de la variable dependiente en vez de estimar por separado la influencia de cada variable independiente. Carl F. Christ, Econometric Models and Methods, Nueva York, John Wiley and Sons, Inc., 1968, pp. 159-389. Se seleccionaron las variables y la forma de éstas principalmente con base en la información disponible. Variables tales como camas de hospital, escala de honorarios, el porciento de especialistas,(12) y la existencia de escuelas de medicina,(13) afectan y son afectadas por el número de médicos por 10,000 habitantes y por esta razón se excluyeron. A continuación se resumen las variables incluidas y las relaciones esperadas. (12). El efecto de estas variables puede incluirse indirectamente en la gran cantidad de información que contienen las variables independientes. Por ejemplo, la escala de honorarios en el ejercicio privado se correlaciona altamente con la urbanización y el producto per capita. Las escalas de salarios en el IMSS y en otros servicios son uniformes en todo el país con algunas excepciones referidas al mayor costo de la vida en algunas entidades fronterizas. Pero el ingreso complementario proveniente del ejercicio privado de médicos que trabajan en dichos servicios se puede lograr principalmente en las grandes ciudades, y de todas maneras es donde se concentra la mayoría de los servicios. (13). En algunas regiones de México la viabilidad de una escuela de medicina está determinada, en cierto grado, por la presencia de médicos suficientes en la región inmediata que puedan ofrecerse como profesores de tiempo parcial. 1. Porciento urbano : localidades de 2,500 y más. Esta variable abarca influencias directas tales como la preferencia de los médicos por ciudades, los efectos de concentración de los grandes centros médicos, y los efectos de demostración en el consumo de atención médica. También actúa como variable de aproximación (parcial) del nivel de desarrollo, el ingreso y la educación; de los patrones de morbilidad y mortalidad; del tamaño, número, poder económico y político de los grupos que tienen acceso (o acceso potencial) a los servicios de salud, y de otros factores que afectan a la demanda. Se incluyen índices específicos de que se dispone para algunos de estos factores, pero no respecto al resto. 2. Producto bruto estatal per capita. Esta variable mide el desarrollo económico y la capacidad para sostener médicos con ejercicio privado de la profesión. También funciona como una aproximación parcial de la influencia de la educación, la estructura ocupacional, la aculturación, la extensión de grupos organizados, etc., en la misma forma que la variable urbana. No hay información disponible para comprobar si el producto per capita es afectado por la morbilidad (como lo pueden sugerir los estudios sobre el costo "residual" y económico de la enfermedad) o si la morbilidad es afectada por la oferta de médicos. Por lo tanto, al considerar que el producto es independiente de la oferta de médicos, es necesario suponer -lo que implícitamente se supone en otros estudios de demanda- que el efecto, si es que existe, no es suficiente para sesgar los resultados. El producto per capita no es la mejor expresión del ingreso dadas las diferencias en la distribución del ingreso entre las entidades, pero es la única disponible. Otras variables que se examinan a continuación funcionan como aproximaciones a la distribución del ingreso. 3. Porciento de la población con 12 o más años de educación. Esta variable representa los cambios en los gustos, la capacidad de ganar ingreso, el conocimiento rudimentario de la medicina moderna y la voluntad de utilizarla.(14) Se eligió el nivel educativo en vez del flujo educativo debido a que el tamaño y el producto de la educación media y la superior son menos importantes en cuanto a significar demanda de médicos en un año dado que la proporción de egresados de dichos ciclos respecto a la población total. El porciento de alfabetos y el porciento que ha alcanzado otros niveles de educación -6, 10, 16 años, hete.- serían variables interesantes de sustitución o suplemento en el modelo. Pero los datos sobre alfabetismo en México no son confiables y la experimentación con otras formas de la variable educación sobrepasa los límites de esta parte del análisis. (14). Numéricamente esta variable y las restantes no son completamente independientes del número de médicos por 10,000 habitantes por el simple hecho de que los médicos mismos tienen más de 12 años de educación, viven en viviendas con facilidades de drenaje y desagüe, consumen alimentos con alto contenido de proteínas y pan de trigo, y usan zapatos. Pero los médicos también utilizan médicos, y debido a que este número es pequeño, la oferta de médicos no se restó al calcular los valores de las variables en cada entidad. 4. Porciento de la población que habita viviendas sin facilidades de drenaje y desagüe. Esta variable funciona como aproximación al ingreso, la distribución del ingreso, los niveles de vida y las condiciones del medio ambiente. 5. Porciento de la población de más de un año que por costumbre come alimentos con alto contenido de proteínas. Esta variable funciona como aproximación a la morbilidad, la participación en la economía monetaria, el ingreso, la distribución del ingreso, y la educación y la aculturación. Los estudios a nivel de poblado señalan que las diferencias en la dieta, en particular el consumo de artículos de "lujo" con alto contenido de proteínas tales como leche y huevos, son el resultado de diferencias en la educación, la aculturación y la riqueza -y no de la riqueza por sí sola.(15) (15). Oscar Lewis, Life in a Mexican Village : Tepoztlán Restudied, Urbana, University of Illinois Press, 1963, p. 189. 6. Porciento de la población de más de un año que por costumbre come pan de trigo. Esta variable funciona como aproximación a la aculturación, la participación en la economía nacional, el ingreso y la distribución del ingreso. La mayoría de los mexicanos, aun los ricos, todavía comen la tradicional tortilla de maíz. Pero el consumo general de pan de trigo junto con, o en vez de tortillas, es un indicador de la posición social y económica y de la aculturación, que es relativamente independiente de la naturaleza de la agricultura local.(16) Por ejemplo, el estado de Guanajuato es el segundo productor de trigo en México, y el estado de Yucatán no produce trigo; sin embargo, en 1960 la proporción de la población que por lo general comía pan de trigo era menos del 46% en Guanajuato y más del 92% en Yucatán.(17) (16). El consumo de pan de trigo como indicador de cambio económico y cultural se discute en Lewis. Op. Cit., p. 189; James W. Wilkie, The Mexican Revolution : Federal Expenditure and Social Change Since 1910, Berkeley, University of California Press, 1967, p. 225- y Joel L. Johnson y Howard M. Smolkin, "Poverty Indicators in Rural Mexico", trabajo inédito, Woodrow Wilson School of Public and International Affairs. Princeton University, 1966, pp. 7-9. (17). Esto se señala en Johnson y Smolkin, op. Cit. p. 9. 7. Porciento de la población de más de un año que por costumbre usa zapatos. Esta variable funciona como aproximación a la aculturación, la estructura ocupacional y la distribución del ingreso, pero no del clima.(18) La mayoría de los mexicanos, excepto los muy pobres, poseen por lo menos un par de zapatos, pero la gente de edad avanzada y las familias rurales en las comunidades tradicionales los guardan para ocasiones especiales y usan huaraches o andan descalzos la mayor parte del tiempo.(19) (18). Las correlaciones simples entre el porciento de población que por costumbre usa zapatos e indicadores del clima tales como la altitud (-0.19818), fluctuaciones de la temperatura (-0.24615) y temperatura media (0.04451) no son significativas al nivel de .05. Por lo tanto, la edad y los factores económicos y culturales parecen ser los factores determinantes del uso de zapatos. El significado de las costumbres respecto a zapatos se examina en Lewis, op. cit., p. 206. (19). El censo pregunta a cada entrevistado si por costumbre utiliza zapatos, come pan de trigo, etc. Existe un peligro de un sesgo hacia arriba en las cifras del censo, especialmente en lo que se refiere a zapatos, Si la frase por costumbre se interpreta libremente por parte del entrevistado que quiera parecer "moderno" en su vestido y gusto. Véase Johnson y Smolkin, op. cit., p. 33.
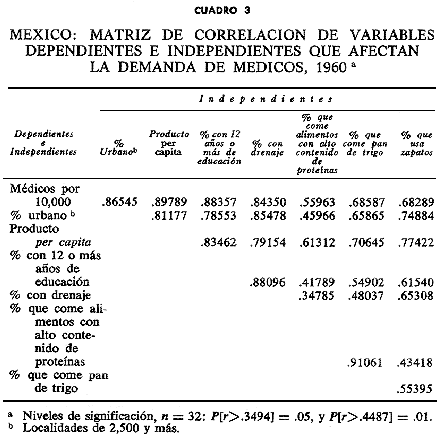
III. RESULTADOS DEL ANALISIS DE REGRESION Contenido En el cuadro I del apéndice se proporcionan los valores de las siete variables independientes y de las variables dependientes en 1960. Los valores correspondientes a las variables de 1965 se proporcionan en el cuadro II del apéndice. Con esta información es posible hacer pruebas tanto para relaciones concurrentes como de rezago calculando primero los cocientes de médicos entre población en 1960 respecto a las siete variables independientes en 1960, y luego los cocientes de médicos entre población en 1965 respecto a las siete independientes en 1960. En el último caso la hipótesis sería que los incrementos de la demanda (y las respuestas a la demanda) están rezagados con respecto a los incrementos del ingreso, la urbanización, el nivel educativo, etc. Las relaciones podrían, de hecho, ser muy complejas, dejando sentirse de inmediato los efectos de algunas variables y retardándose los efectos de otras por una generación. En esta ocasión sólo es posible una prueba preliminar que tiene como hipótesis un rezago de cinco años en los efectos de todas las variables. En los cuadros 3 y 4 se señalan las correlaciones simples y en el cuadro 5 los resultados de la principal ecuación de regresión. Esta ecuación establece que las variaciones en el número de médicos por 10,000 habitantes en 1965 se "explican" por las variaciones ocurridas en 1960 en el nivel educativo alcanzado, la urzanización y el consumo de proteínas, en este orden. La agregación de otras variables redujo R² e incrementó el error estándar de estimación de la ecuación.
CUADRO 4 MEXICO : MATRIZ DE CORRELACION CON VARIABLES
El valor 141.0 para F es significativo al nivel de .01, y el valor .931 para R² es notablemente alto en un análisis transversal-dejando menos del 7% de la varianza en las variables dependientes sin explicación.(20) El error estándar de estimación de la ecuación equivalente a 17.4% de la media de la variable dependiente, indica que las observaciones se encuentran un tanto dispersas alrededor de la línea de regresión. Los valores t correspondientes a las tres variables independientes son significativos al nivel de .01, e indican que las tres variables contienen por lo menos alguna información por separado y, por lo tanto, que un alto R² no es simplemente el resultado de multicolinealidad en los datos. Sin embargo, el determinar precisamente cuál es la información significativa requeriría una investigación que se encuentra fuera de los alcances de este trabajo y de la naturaleza de los datos disponibles. Cada variable independiente incluida en el modelo es una medida bastante general del desarrollo económico y social y funciona como variable aproximada para otras medidas. Inferencias detalladas sobre la causalidad requeriría índices limitados y discretos para cada medida y una exploración profunda de numerosas relaciones potenciales. Sin embargo, es significativo que una ecuación de rezago resultó ser mejor que una ecuación concurrente. En los pueblos y las ciudades sí persisten percepciones y conceptos tradicionales respecto a la enfermedad y la curación, aun entre los recién educados que tienen algún conocimiento de la medicina moderna y que tienen voluntad de consultar un médico como último recurso. Además, probablemente hay un rezago en la respuesta de los médicos privados a un cambio en el nivel de la demanda, y un rezago obvio en la respuesta del gobierno y en la de las escuelas de medicina, en la mayoría de las cuales se requieren por lo menos cinco años para graduarse como médico. Con mejores datos sería posible hacer pruebas con respecto a rezagos más largos o más cortos (si los hay) en los efectos de cada variable, y distinguir rezagos en la demanda a partir de rezagos en la respuesta a una demanda cambiada. (20) El alto R² de esta ecuación y las subsiguientes se explica parcialmente por el hecho de que el valor de las variables dependientes en el Distrito Federal es casi 50% más alto que el valor de la segunda observación más alta.
Crecimiento de la población. El factor más importante que afecta a la demanda es el crecimiento de la población. Las proyecciones de población pronostican un crecimiento de 42.8 millones en 1965 a 51.1 en 1970, 60.9 en 1975 y 71.9 en 1980.(21) Se puede calcular la amplitud del impacto de este crecimiento en la demanda de médicos en cada entidad : I) manteniendo constantes los cocientes de 1965, 2) manteniendo constantes los cocientes de 1960, y 3) manteniendo constantes los cocientes más elevados, sean de 1960 o 1965 (en el supuesto de que si el cociente de una entidad disminuye entre 1960 y 1965, el cociente más elevado de 1960 debería mantenerse constante como el nivel comprobado de demanda mínima). En los cuadros III, IV y V del apéndice se proporcionan los resultados por entidades. Los totales nacionales agregados pronosticados para 1980 se señalan a continuación : (21) R. Benítez Zenteno y G. Cabrera Acevedo, Op. cit., pp. 184-185. Médicos
Así, con la base de 25,062 correspondientes a 1965, el número de médicos tendría que incrementarse en un 77 a 86% sólo para mantenerse en equilibrio con el crecimiento de la población proyectada a través de 15 años. La necesidad de recién graduados de las escuelas médicas sería más elevada aún.(22) Pero si las relaciones permanecen constantes y no hay mejoras en la productividad, la oferta no alcanzaría a la demanda. El ingreso, la urbanización y el nivel educativo también aumentan, y el mismo número de médicos por 10,000 habitantes tendría que afrontar un incremento en la demanda por parte de una proporción creciente de la población. (22). Más adelante se hacen estimaciones del desperdicio y el número de nuevos graduados requeridos. Ecuaciones de una y dos variables. No se puede utilizar el modelo de rezago al proyectar la demanda dada la dificultad para estimar los valores futuros de las tres variables independientes, en particular el nivel educativo y el consumo de proteínas, respecto a cada entidad en cada año meta. Los errores que se introdujeran contrarrestarían con exceso el alto poder predictivo de la ecuación. Se tiene que usar en su lugar una ecuación más sencilla con un poder de pronóstico menor, pero basada en una o dos variables independientes que sean relativamente más fáciles de proyectar. La mejor elección es una ecuación basada en una o dos formas de la variable urbana. La urbanización afecta directamente la demanda de médicos y funciona como variable aproximada de otras medidas de desarrollo económico y social. De cualquier manera se tiene que proyectar la población para convertir los cocientes pronosticados en cantidades reales de médicos y al mismo tiempo se pueden hacer proyecciones por separado para la población urbana y rural con poco riesgo de errores adicionales. De hecho, las proyecciones intermedias contienen proyecciones separadas para las poblaciones urbanas y rurales en cada entidad entre 1965 y 1980. Las ecuaciones más sencillas contienen sólo la variable urbana y una constante, en la forma general
donde :
De estas ecuaciones, aun las mejores representan una disminución grande del poder de pronóstico con respecto al modelo desarrollado en la primera parte de este trabajo. La ecuación 1.1 deja el 25% de la varianza en las relaciones de médicos a población de 1960 "sin explicación", y el error estándar de estimación de la ecuación es igual al 33.4% de la media de Y1. Las ecuaciones 1.2 y 1.3 -las ecuaciones concurrentes y de rezago que pronostican los cocientes en 1965- se ajustan menos. El uso de cualquiera de estas ecuaciones para pronosticar cocientes futuros podría introducir un error considerable en un período de proyección de 15 años. Los diagramas de dispersión de urbanización y los cocientes de médicos entre población en 1960 y 1965 indican que un modelo no lineal podría producir mejor ajuste. Se probó dicha posibilidad con el modelo que tiene la forma general, Y = a + + bX + c(X²) y se desarrollaron otra vez tres ecuaciones : R² Error estándar 2.1) 1960 : Y1 = 2.8470 + 0.002098(U²) - 0.07375U1 0.82330 1.30620 Las curvas trazadas a través de los valores Y que estiman las tres ecuaciones son de forma cóncava, lo que sugiere que el cociente de médicos entre población al principio aumenta con menor rapidez que la población urbana y luego más rápidamente después de que se hayan alcanzado niveles intermedios de urbanización -entre 45 y 65%. La ecuación 2.2 tiene el mayor poder de pronóstico de todas las ecuaciones que contienen la variable urbana y/o la variable urbana al cuadrado y con datos de 1960 y 1965. Se probaron otras ecuaciones, incluidas : Y1 = a + b (U²), 2 Y2 = a + b (U²), Y2 = a + b (U²), Y2 = a + bU1 + CU2 y 2 1 Y2 = a + bU1 + + C(U1) + dU2 + e(U²); pero ninguna tuvo un error 2 _ estándar de estimación más bajo o una R² más elevada que la ecuación 2.2. La ecuación 2.2 deja menos del 16% de la varianza en Y2 "sin explicación", y el error estándar de estimación es igual al 27.4% de la media de Y2. Dado que la ecuación está basada además en la información más reciente disponible, es la elección más acertada para proyectar los cocientes y el número de médicos en 1970, 1975 y 1980. Una prueba final. Quedan dos problemas. Uno es la utilización de ecuaciones de sección transversal para pronosticar el futuro, y el otro es el elevado error estándar de estimación de la ecuación 2.2. Una prueba parcial respecto al riesgo de error que se origina en cualquiera de estos problemas sería utilizar las ecuaciones de 1960 para pronosticar el número de médicos en 1965 y comparar los pronósticos con la información real de ese año. Debido a que las ecuaciones de 1960 son de sección transversal con errores estándar de estimación más altos que la ecuación 2.2, los resultados dan alguna indicación sobre el nivel mínimo de exactitud que se puede esperar de la ecuación 2.2 en un período de proyección de cinco años. Se solucionaron las ecuaciones de 1960 utilizando las proyecciones de la población urbana en cada entidad en 1965 para calcular los cocientes, y las proyecciones de la población total de la entidad para calcular el número de médicos. En el cuadro 6 se señalan los resultados con la ecuación 1.1, y en el cuadro 7 los resultados con la ecuación 2.1. Como era de esperar, la ecuación lineal 1.1 es la menos exacta de las dos a nivel de entidad. Pronostica demasiados pocos médicos en las entidades intermedias. El error combinado es 6,695 médicos, o sea 26.7% del total nacional real en 1965. La ecuación no lineal 2.1 es más exacta a nivel de entidad, aunque también pronostica demasiados médicos para las entidades intermedias donde los cocientes reales disminuyeron durante los cinco años. El error combinado es de 4,150 médicos, o sea 16.6% del total nacional real en 1965.
CUADRO 6 MEXICO : PROYECCION DE LA DEMANDA DE MEDICOS EN 1965(a)
Ambas ecuaciones tienen menor exactitud en los estados de México y Tlaxcala, donde los pronósticos exceden el número real de médicos en más de 100%. Pero México y Tlaxcala son precisamente los estados en donde la definición censal de urbanización (localidades de 2,500 y más) sobreestima en mayor medida el tamaño real de la población urbana. A nivel nacional, los errores tienden a compensarse. La ecuación 1.1 se aproxima en 147 médicos, o sea 0.6% del total nacional real en 1965. La ecuación 2.1 se aleja en 1,448 médicos, o sea 5.8%, y la mayor parte de este error se puede encontrar en las entidades intermedias donde las relaciones disminuyeron entre 1960 y 1965 aunque probablemente no disminuyó la demanda real. Por lo tanto, las anormalidades son explicables y los resultados son congruentes con las expectativas y con las pruebas estadísticas, y acusan exactitud asombrosa a nivel nacional. De allí que las ecuaciones desarrolladas y las proyecciones de población puedan ser utilizadas con alguna confianza para pronosticar los cocientes y el número de médicos en 1970, 1975 y 1980. Proyecciones. Para las proyecciones se utilizaron ecuaciones de ambos años base para poder establecer los límites superior e inferior de la demanda. La ecuación 2.2 fija el límite inferior dado que está basada en la estructura y la distribución de la demanda en 1965. Las ecuaciones 1.1 y 2.1 fijan el límite superior debido a que se basan en la estructura de 1960. La ecuación lineal 1.1 de 1960 pronostica la demanda más cercana al total pero es relativamente inexacta a nivel de entidad. La ecuación no lineal 2.1 _pronostica una demanda casi tan cercana al total y tiene un R² más elevado y un error estándar de estimación más bajo. Esta ecuación es la elección lógica para fijar el límite superior de la demanda. Se solucionaron ambas ecuaciones utilizando las proyecciones de población urbana en 1970, 1975 y 1980 para calcular los cocientes y las proyecciones de la población total por entidad para calcular el número de médicos. Sin embargo, en los casos en que los cocientes de médicos entre población pronosticados en 1970, 1975 y 1980 eran inferiores a los cocientes reales de la entidad en 1965 ó 1960, el cociente real más elevado se utilizó para calcular el número de médicos y enfermeras bajo el supuesto de la demanda mínima comprobada. En los cuadros VI y VII del apéndice, se señalan los resultados completos. El cuadro 8 señala el número total de médicos proyectados en las ecuaciones 2.2 y 2.1 en cada año meta.
CUADRO 7 MEXICO : PROYECCION DE LA DEMANDA DE MEDICOS EN1965(a)
MEXICO : LIMITE DE VARIACION PROYECTADA
Los incrementos proyectados son de hecho muy grandes. Sin cambios importantes en la estructura de la atención de la salud, el número de médicos tendría que aumentar de un 117 a un 134% para hacer frente a la demanda en 1980. Todavía se origina la mayor parte del incremento en el crecimiento de la población. Pero a la urbanización -que funciona como variable aproximada del desarrollo económico y social- puede atribuirse más de una cuarta parte del total pronosticado por la ecuación 2.2 y más de una tercera parte del total, pronosticado por la ecuación 2.1. Si fuera satisfecha esta demanda entonces el nivel nacional aumentaría de 5.9 médicos por 10,000 habitantes en 1965 a entre 7.6 y 8.2 en 1980. Estimación del desperdicio. Se puede estimar el número de nuevos médicos necesarios para alcanzar dichos cocientes utilizando la tasa de desperdicio del acervo existente entre enero 1º de 1960 y diciembre 31 de 1965 calculado como sigue :
donde :
(23). El recuento en 1960 se hizo en junio 1º e indicó un total de 20,590 médicos. Este total no incluye los graduados en 1960, mientras que el total en 1965 (tomado en diciembre 31) sí incluye a los graduados en 1965. Con objeto de cubrir un total de seis años de graduación y desperdicio en vez de seis años de graduación y cinco años y cinco meses de desperdicio, fue necesario ajustar el total de 1960 a enero 1º de 1960, estimando el monto de desperdicio que ocurrió entre enero 1º y junio 8 de ese año. Se hizo una estimación mínima mediante la resolución de la fórmula utilizando el total sin ajuste para 1960 y un período de desperdicio de seis años. El resultado fue una tasa compuesta de desperdicio de aproximadamente el 1.8% anual que dio una estimación de 186 médicos perdidos entre enero y junio. El total de 1960 se aumentó entonces de 20,590 a 20,776. (24). Apéndice, cuadro VIII. (25). Estimado a partir de información en Organización Panamericana de la Salud, Migration of Health Personnel, Scientists and Engineers from Latin America, Washington, D. C., Scientific Públication, Núm. 142, septiembre de 1966, pp. 26 y 33. (26). Calculado a partir de información en el Apéndice, cuadro VIII, y Huerta Maldonado, Op. cit., 3ª ed., p. 5.
El valor de Rt+n para diciembre 31 de 1965 fue 0.89069, lo cual da una tasa compuesta de desperdicio de médicos del 1.9% anual durante los seis años.(27) (27). Determinado con base en tablas de interés compuesto. El cuadro 9 señala e] número de médicos que deben graduarse en México en cada período de proyección para satisfacer la demanda proyectada al final del período y para cubrir el desperdicio estimado durante el mismo; suponiendo 1) que el desperdicio en la fuerza de trabajo sigue siendo del 1.9% al año, 2) que la repatriación de estudiantes extranjeros, la emigración de mexicanos y el número de los que no ejercen continúa reclamando un promedio de 14% de la producción interna en el período de cinco años, y 3) que los que regresan del extranjero continúan complementando el número de egresados internos (bruto) con un promedio de 3.8% en cada período de cinco años.(28) (28). La estimación del regreso de médicos mexicanos (y la inmigración de médicos extranjeros) del exterior entre 1960 y 1965 (õF) fue igual al 3 8% de los médicos graduados en México (õG) durante el mismo periodo.
CUADRO 9 MEXICO : NUMERO DE GRADUADOS REQUERIDOS DE LAS ESCUELAS DE MEDICINA PARA SATISFACER LA DEMANDA EN CADA PERIODO DE PROYECCION(a)
(b) Véase el cuadro VIII. (c) Este requerimiento para 1970 es alto en forma desproporcionada debido a que la proyección de demanda de la cual se derivó fue calculada, para 1960, a partir de la ecuación 2.1. Cuando se usa este tipo de ecuación, se considera que las escuelas de medicina deben cubrir un "déficit" implícito en la reducción de los coeficientes entre 1960 y 1965, así como mantenerse al ritmo de una demanda proyectada (mayor) para el período 1966-1970.
La pregunta inmediata es si las escuelas de medicina pueden satisfacer esta demanda. Una proyección lineal simple del número de estudiantes que cada año aprueban el examen profesional de medicina señala que tal y como funcionan actualmente las escuelas de medicina no podrán satisfacerla. La proyección señala que 36,900 estudiantes aprobarán los exámenes profesionales de medicina entre 1966 y 1980(29) -o sea de 6,000 a 12,000 menos de los que se "demandarían" en un lapso de 15 años. (29). Esta proyección se basa en el número de estudiantes que terminan sus cursos (pasantes) en las escuelas de medicina mexicanas entre 1960 y 1967 (inclusive); datos recopilados por Adrián Lajous Vargas, Aspectos de la educación superior y el empleo de profesionistas en México, 1959-1967, tesis profesional, México, Universidad Nacional Autónoma de México. Escuela Nacional de Economía, 1967. La regresión del número de pasantes y tiempo (año 1, 2, 3, etc.) produjo un R² de 0.85943 y una F de 36.7 -ambos significativos a nivel de .01 (con 7 grados de libertad.) Se utilizó la ecuación de regresión para proyectar el número de pasantes cada año hasta 1980, y se calculó el número de graduados recibidos suponiendo que el 90% de los pasantes de cada año aprobarían los exámenes profesionales de medicina un año más tarde. (El porciento real de pasantes que aprobaron los exámenes profesionales entre 1961 y 1965 -suponiendo un año de rezago- fue 85.6 calculado comparando el número de pasantes en Lajous Vargas, op. cit., con el número de médicos un año después, señalados en el Apéndice, cuadro VIII). Los resultados de cada período de proyección fueron los siguientes : 1966-1970 9,901 médicos nuevos; 1971-1975, 12,267 médicos nuevos; y 1976-1980, 15,048 médicos nuevos Se necesita investigación respecto a los costos y rendimientos, respecto a cambios en el sistema educativo y la estructura de incentivos. En las escuelas de medicina muchos estudiantes desertan o son reprobados antes de graduarse. Por ejemplo, de los estudiantes que ingresaron en 1962, aproximadamente el 76% completó el total de cinco años de cursos en la Escuela Médico Militar, 56% lo hizo en la Universidad Nacional Autónoma de México, 28% en la Universidad Autónoma de San Luis Potosí y 14% en la Universidad Autónoma de Puebla.(30) El promedio nacional fue 49%. (30). Calculado a partir de información inédita recopilada por la Asociación Nacional de Universidades e Institutos de Enseñanza Superior. Los cálculos son aproximados debido a que no se pueden distinguir los repetidores. Se estima que la tasa de repetición es alta. Las tasas de retención son bajas por muchas razones, incluida la baja calidad de las escuelas preparatorias, la deficiente selección de los aspirantes,(31) la aglomeración, profesores mal adiestrados y de tiempo parcial, la cantidad y dificultad de los cursos, las altas tasas de repetición y el sacrificio inmediato de ingresos que supone hacer la carrera médica,(32) así como la poca ventaja relativa en cuanto al ingreso que se obtiene posteriormente en comparación con los de los graduados de escuelas profesionales menos exigentes. (31). Una excepción es la Escuela Médico Militar que con conciencia ha seleccionado a sus aspirantes desde 1932. Véase Asociación Nacional de Universidades e Institutos de Enseñanza Superior, Memoria de la Quinta Reunión de la Asociación Mexicana de Facultades y Escuelas de Medicina, México, 1962, pp. 91-106. (32). Otra vez, la Escuela Médico Militar es una excepción. Normalmente no se permite la repetición de los cursos. Se espera que los estudiantes terminen sus cursos de cinco arios y mientras que estudian se les provee de cuarto, alimento, vestido y una pequeña cantidad de dinero. No hay duda de que si se verificaran cambios en el sistema educativo y en la estructura de incentivos, se incrementaría la proporción de estudiantes que se gradúan, y la proporción de graduados que ejercen la medicina en México. Con cambios grandes, se podría satisfacer la demanda proyectada. Por ejemplo, en las escuelas de medicina sería necesario elevar la tasa media de retención de 49% a entre 57 y 65%. Pero no son claras las implicaciones de costo de tal programa. Una mejor selección de aspirantes y la modificación de los planes de estudio podrían reducir los costos directos y sociales por graduado;(33) con profesores de tiempo completo y clases más pequeñas se podría incrementar el costo. Y cualquier costo -aun el de entrenar sólo 36,900 médicos- debe contrapesarse con otras demandas sobre los fondos públicos implícitos en un crecimiento rápido de la población y en una gran población dependiente durante el período de la proyección. (33). Obviamente se incrementaría el costo por estudiante. Los médicos son los profesionales de la salud que son más costosos de entrenar y emplear. Actualmente México depende exclusivamente de los médicos para la atención médica. Las proyecciones indican algunos de los costos y la dificultad de continuar esta dependencia en el futuro. Además, es muy probable que exista un desajuste entre la estructura de la atención médica y los problemas médicos de la población. En gran parte de México persisten enfermedades que resultan del medio ambiente y de deficiencias en la dieta. Puede ser que el énfasis en la medicina curativa y en los médicos, y en los especialistas y en los hospitales necesarios para proporcionarla, pueda ser apropiado después de que se hayan reducido estas enfermedades, pero no antes. La población quizá esté condicionada a esperar y utilizar un sistema de atención médica que ha sido desarrollado anticipándose a sus necesidades médicas en vez de haberse desarrollado a la par de éstas -un sistema que muchos no tienen medios de procurarse y que posiblemente el gobierno no pueda proporcionarles. Por sobre todo, hace falta investigar esta posibilidad.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||