|
Los resultados y perspectivas sobre desarrollo e investigación curricular que presentamos han sido elaborados en la Universidad Autónoma Metropolitana-Azcapotzalco. Esta unidad universitaria cuenta con tres divisiones, las cuales se componen de un cierto número de departamentos. En la División de Ciencias Básicas e Ingeniería, el Departamento de Ciencias Básicas es responsable de la impartición de determinados cursos que conforman un tronco común; es decir, esos cursos son obligatorios para los alumnos que inician sus estudios de ingeniería en dicha división. La reflexión sobre el currículum universitario alcanzó una magnitud tal en la UAM que se convirtió en su actividad central durante muchos años. Causas de lo anterior radican -naturalmente- en que dicha universidad, al ser creada (1974), requirió de la elaboración de planes, programas, perfiles de los egresados, etcétera. El proceso de reflexión curricular mantuvo para nuestro equipo de trabajo una faceta fundamental; nos vimos obligados a cristalizar reflexiones en planes y programas de estudio. Pronto esta conjugación de actividades nos fue empujando a revisar planteamientos o esquemas que empleábamos para el diseño curricular. Influyeron de manera determinante en la revisión de nuestros planteamientos los siguientes hechos: Las metas educativas que posee un curso no se comportan como objetos materiales diseñados para satisfacer ciertos usos. Como consecuencia de lo anterior, en cuanto dichas metas son puestas en circulación sufren distintas apropiaciones y diferentes reflejos, derivados de las diversas maneras de pensar y actuar de quienes efectúan la apropiación o el reflejo. También presenta dificultad la elaboración y adecuación de metas educativas que serán utilizadas simultáneamente por distintos usuarios, v. gr., ingenieros civiles y electrónicos, o bien sociólogos rurales y administradores de empresas. Además, el proceso de enseñanza-aprendizaje debe llevarse a cabo con alumnos cuya formación e información se ha realizado en diferentes niveles educativos sin existir, necesariamente, una adecuada articulación entre cada nivel y de todos ellos entre sí. El presente trabajo tiene como finalidad exponer un esquema, bastante sencillo, el cual hemos empleado como guía en el terreno del diseño curricular; también se expondrán algunos resultados derivados del uso de dicho esquema. Unas palabras acerca de las limitaciones de este trabajo: no trataremos aquí la parte del diseño curricular referente a la elaboración de metas y objetivos que una universidad desea depositar en sus egresados; es decir, el trabajo está enfocado hacia el diseño, confrontación y evaluación curricular de materias que son enseñadas durante la estancia universitaria del alumno, y no hacia el diseño, confrontación y evaluación del currículum en cuanto a su posible correspondencia o adecuación a las necesidades sociales o a las del aparato productivo. Nuestra intención es, entonces, enunciar y desglosar algunos elementos que hemos tomado en cuenta para diseñar un curso o evaluar una colección de ellos. En las conclusiones ubicaremos estas actividades en el tema más general de currículum. Los elementos a que haremos mención son los siguientes:
A continuación discutiremos en cierto detalle cada uno de los puntos arriba mencionados.
1. Como nosotros estamos interesados primordialmente en la articulación de la matemática en el currículum de diversas carreras, es natural que busquemos establecer los nexos entre el espectro de la ciencia matemática y las otras áreas. Para ello hemos elegido ponernos decididamente en la perspectiva de andar el camino que deberán recorrer inexorablemente nuestros alumnos en la universidad; es decir, hemos decidido enfrentarnos a la bibliografía que ellos deberán manejar, tanto si pertenecen a tal o cual carrera como a una especialidad dentro de alguna de las carreras que ofrece la UAM-A. La idea básica de emprenderla con la bibliografía a que será expuesto el estudiante es prepararle el camino en cursos anteriores, de tal manera que las exigencias de su carrera -o especialidad- no lo tomen desorientado en cuanto al empleo específico de conceptos matemáticos fundamentales, o en cuanto a la comprensión consciente de los mismos. Tanto por la extensión de la bibliografía, como para hacer más eficaz la labor, es necesario indagar y seleccionar aquella parte que sea la más fundamental o la más clásica para la materia en cuestión. Así, hemos tomado como fuente primordial para elaborar currículum y programas aquella parte de la cultura conocida bajo el rubro vago y genérico de "matemáticas universitarias". 2. Sin embargo, la estrategia esbozada en el párrafo anterior está aunada a esta otra perspectiva. La bibliografía que escudriñamos deberá proporcionarnos no sólo los temas de matemáticas sino, también, cómo y de qué manera son empleados dichos temas, en las diversas áreas (digamos probabilidad y estadística en análisis de señales). Así, al terminar esta actividad deberemos contar con tres conocimientos básicos acerca de la bibliografía: el material fundamental (matemáticas), que es indispensable para la comprensión de la bibliografía; el manejo de variados y típicos ejemplos de cómo es el empleo del material fundamental en ciertas disciplinas, y la profundidad con que el susodicho material fundamental es requerido. En resumen, la pretensión central de los puntos 1 y 2 -a los cuales llamaremos inmersión y especificidad respectivamente- puede frasearse así. Preparar el establecimiento de una propuesta curricular aportando dos soportes del mismo: uno, las áreas de la matemática que serán empleados, los temas fundamentales y el nivel de profundidad que son exigidos por los distintos usuarios; dos, esbozar en los programas correspondientes propuestas de ejemplos, ejercicios y problemas con un gran componente de concreción. En seguida expondremos una aplicación de estos dos puntos a la carrera de Economía en la UAM-A. Una versión completa de aquélla fue presentada bajo el nombre de metodología de inmersión; una aplicación, durante el IV Congreso Internacional de Educación en Matemáticas, Berkeley, California, EE. UU. Pasemos a describir la labor efectuada: el estudio de asignaturas vigente en el Departamento de Economía nos llevó a la elección de ocho cursos de teoría económica (cuatro de micro y cuatro de macroeconomía), así que analizamos los textos correspondientes según la bibliografía de dichos cursos. Como hemos dicho antes, esto lo realizamos no sólo con el fin de agrupar en grandes temas los contenidos matemáticos presentes en los textos, sino también tomando en cuenta la presentación de estos contenidos al ser utilizados en el seno de la Economía. La bibliografía mostró que el empleo de conceptos fundamentales, propios de esta disciplina, consistía en utilizarlos como herramienta de análisis de situaciones simples, concretándose a niveles de operatividad elementales. Esto difiere de manera notable con los contenidos de los programas que exigen técnicas complejas en cuanto a operatividad y una carencia de aplicaciones de esos conceptos a la Economía. También en la bibliografía se encontraron conceptos con una aplicación sistemática en diversas áreas de la Economía. A pesar de su empleo, amplio y reiterado, dichos conceptos no se encontraron en ninguno de los puntos que constituyen el programa. Asimismo, del análisis bibliográfico se concluyó que existían programas completos cuyo enfoque se apartaba totalmente del contexto académico de los estudiantes de Economía. En otras palabras, la presentación de conceptos y resultados matemáticos en estos programas se efectúa mediante un camino abstracto y categórico, a pesar de existir caminos conocidos que sin mengua en la exactitud proporcionan los mismos conceptos y resultados. Otra aplicación de estos dos puntos -inmersión y especificidad- la hemos realizado al adentrarnos en la actividad escolar llamada prácticas de laboratorio.(1) (1) Esta parte la hemos desarrollado en compañía del Físico René Molnar de la Parra, profesor de la UAM-A. Además de los puntos comunes con la enseñanza teórica -de pizarrón-, los cursos de laboratorio mantienen, según la labor que realizamos en estos últimos cursos, las características siguientes:
Por lo anterior, decidimos abordar este renglón educativo mediante el estudio en detalle, a fondo, de un problema en el cual confluyeran variados aspectos de la técnica contemporánea. Es así como elegimos estudiar el circuito R-L,C como una serie de circuitos derivados de un problema: el estudio de una bobina. En este estudio hemos querido mostrar el empleo de conceptos eléctricos (física), cálculo y ecuaciones diferenciales (matemáticas) y redes (ingeniería) de una manera entrelazada y exigiendo que las predicciones y modelos sean contrastados con los resultados experimentales y, recíprocamente, exigiendo la explicación pertinente sobre determinadas observaciones; es decir, hemos querido reflejar en el material las peculiaridades -especificidades- que observamos durante ocho meses de labor en un laboratorio de física de la UAM-A. 3. Supongamos ahora que hemos localizado un área o tema de matemáticas que deba ser presentado como parte de la formación universitaria.(2) El tema pudo ser bosquejado bajo las directrices expuestas en los puntos 1 y 2. Al ordenar los subtemas que componen el área delimitada surge, de manera natural, la necesidad de presentarla como un todo coherente, ordenado; esto nos obliga, generalmente, a incluir información que si bien no forma parte estricta del tema en cuestión, es indispensable para evitar caer en el diseño de cursos que consistan en simples colecciones de operaciones o técnicas. Aquí debemos estar protegidos, también, contra la "tendencia a un excesivo énfasis en la abstracción dentro de la enseñanza de las Matemáticas".(3) (2) Véase nota 1 de la bibliografía que se presenta al final de este trabajo. En virtud de lo anterior, mantenemos un especial interés en encontrar desarrollos teóricos o demostraciones matemáticas que sin pérdida de consistencia o rigor, sean ilustrativos, accesibles y constructivos. En la búsqueda de tales desarrollos o demostraciones, los siguientes hechos ayudan a discernir entre las múltiples opciones. En distintas áreas es común el empleo de la herramienta matemática para transformar problemas laboriosos en otros cuya complejidad se reduce básicamente a problemas operativos. Más aún, esta herramienta, en general, requiere de un menor número de conceptos y permite resolver una gran diversidad de problemas. Ejemplo de lo anterior lo constituyen la transformada de Laplace y la de Fourier. Otra herramienta que se ha establecido de manera definitiva en el currículum universitario es la de la computación. Lo anterior es especialmente cierto en las diversas ramas de la ingeniería. en donde prácticamente todo problema debe presentarse acompañado de resultados numéricos. Así, de manera inevitable, junto a la computadora se intercalarán al currículum universitario diversas áreas de la matemática (métodos de probabilidad y estadística, ecuaciones no lineales, etcétera) las cuales con anterioridad tenían una presencia bastante reducida, dentro de los planes y programas de estudio. Las ideas desarrolladas en este punto encontraron concreción cuando establecimos una alternativa de programa para un primer curso de ecuaciones diferenciales. Características curriculares fundamentales de este curso son: enfoque de los temas mediante el empleo de métodos operacionales y supresión de conceptos innecesarios para el logro de las metas del programa; aunado a esto, el método operacional proporciona una manera ágil y constructiva para la demostración de un resultado de capital importancia en la teoría y las aplicaciones. 4. El cuarto punto que, a nuestro juicio, también puede ser empleado para modificar y diseñar un currículum lo constituye el tema de la evaluación. Para cumplir cabalmente su empleo en el diseño curricular y la consecuente modificación de los problemas de estudio, la evaluación debe proporcionar información sobre las siguientes dos cuestiones.
Concibiendo entonces la evaluación como parte integrada al proceso de enseñanza-aprendizaje y no como una secuela con carácter puramente selectivo, tal evaluación no sólo debe proporcionar información acerca del aprovechamiento o aprendizaje por parte del alumno, que permita decidir su situación escolar, sino que además debe proveer de elementos objetivos de juicio que indiquen si nuestros objetivos y metas educativas son estadísticamente alcanzables; dificultades en el logro de objetivos, así como la carencia de objetivos que representen conceptos intermedios para el logro de objetivos establecidos en el programa; y qué tan adecuado ha resultado el proceso de enseñanza-aprendizaje en el logro de las metas del programa. De este modo, para que la evaluación contemple los elementos de juicio antes mencionados, deberá satisfacer al menos cuatro condiciones:
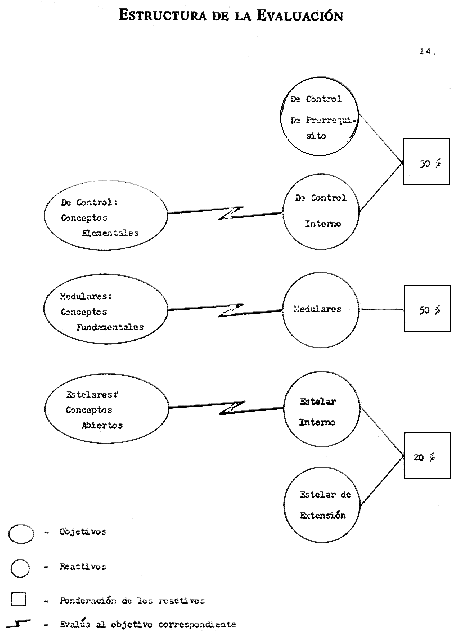
A continuación mostraremos con base en una figura y en forma abreviada la serie de conceptos básicos que empleamos para la evaluación. Definiciones completas y mayor detalle se encuentran en el tema I de la referencia bibliográfica Nº 2 que aparece al final de este trabajo. Con base en estas propuestas se han elaborado exámenes departamentales de los cursos de ecuaciones diferenciales en el Departamento de Ciencias Básicas durante dos trimestres. Los resultados, importa señalarlo, indican tendencias positivas.(4)
(4) El conductor de esta labor es el Prof. Carlos Ulín jiménez, miembro del Departamento de Ciencias Básicas de la UAM-A. 5. En seguida concederemos atención a un tema que hemos denominado "articulación". Este elemento pretende llamar la atención sobre el historial poseído, en término medio, por los estudiantes a su ingreso y durante su estancia en la universidad: el comparar este historial promedio con las metas de los cursos ofrecidos permite contraer un compromiso más consciente entre alumnos, profesores y universidad. Este parámetro también permitirá seleccionar con mayor acierto los proyectos que requieran prioridad como pueden ser: elaborar o no, material de apoyo; elegir técnicas educativas apropiadas, etcétera. Como es fácil notar, este elemento incide de manera específica en la esfera de la continuidad, secuencia e integración de los diversos niveles educativos y en la articulación interna de cada uno de ellos. El siguiente ejemplo proviene de una evaluación aplicada a una muestra representativa de alumnos, con al menos un semestre de permanencia en un centro de enseñanza superior.(5) (5) Este trabajo lo realiza uno de los autores en otro centro de enseñanza superior. La evaluación estaba dirigida esencialmente a obtener datos sobre los conocimientos actuales de matemáticas en los alumnos. Los reactivos valoran conceptos del nivel medio superior con empleo frecuente en la licenciatura; el 91% de los reactivos exigían solamente operatividad por parte del alumno. El examen fue aprobado por el 20% de los alumnos. Todos los alumnos mostraron serias deficiencias en aritmética, cálculo y álgebra. Aunque no pretendemos arrancar conclusión definitiva alguna de exámenes de ubicación como el anterior, sí pretendemos mostrar la urgente necesidad de inhibir la falta de articulación entre la cultura real -en este caso matemática- que poseen los alumnos y aquella que supuestamente deben poseer, al transcurrir sus actividades educativas de acuerdo a un currículum y su concomitante plan -programa- de estudios; también tenemos la hipótesis de que las actividades necesarias para obtener, mantener y desarrollar la articulación a que hemos hecho mención, deben contar con el apoyo decisivo de fuentes universitarias como son las bibliotecas y laboratorios, los cuales, infortunadamente, se mantienen un tanto alejados y en un papel francamente secundario dentro de la vida universitaria. Sin lugar a dudas reconocemos que este inmenso mundo de actividades -que a la universidad debe exigírsele- asumirá una concreción determinada, y no por ello menos universal, en cada una de las universidades del país. 6. Contar con información que contemple en detalle y sin ambigüedad el contenido de cualquier materia del plan de estudios es indispensable para lograr una estrecha articulación entre una materia y otra. Más aún, dicha información es indispensable para identificar los cambios necesarios a que da lugar una modificación del plan o programa de estudios. En estos casos es absolutamente necesario contar con una cuidadosa descomposición de las metas educativas de cada materia en actividades más simples- digamos atómicas-, todo lo cual permite acotar definitivamente las pretensiones de dichas materias. Consecuentemente debemos contar con material para que perfile, con la menor dispersión posible, el qué enseñar. En otras palabras, es necesario ubicar y delimitar con precisión las metas educativas que se pretenden alcanzar en los cursos universitarios de matemáticas. En la enseñanza superior el currículum generalmente está expresado sólo en grandes líneas permitiendo, por lo tanto, una amplia interpretación indhidual por parte de cada profesor.(6) (6) Véase nota 5 de la bibliografía. Un hecho aunado al anterior y con el cual coexistimos en las universidades es el incremento del número de profesores que imparten la misma asignatura; además, de dichos profesores, los de tiempo completo representan un pequeño porcentaje en relación al total. Lo anterior conlleva una limitación extrema en la comunicación de las metas educativas propias de la asignatura, las cuales, entonces, dependerán fundamentalmente de la experiencia y formación de cada uno de los profesores. Esto contribuye, evidentemente, a una falta de homogeneidad en los cursos. Otro fenómeno que se presenta en las universidades, en particular en la UAM, es el establecimiento de troncos comunes en áreas de conocimiento; es decir, la existencia, al inicio de los estudios universitarios, de un conjunto de materias comunes para las diferentes carreras que constituyen dicha área. Por ejemplo, el Departamento de Ciencias Básicas de la División de Ciencias Básicas e Ingeniería de la UAM-A está responsabilizado de materias correspondientes al tronco común; más aún, las evaluaciones respectivas se realizan en forma departamental; así, los estudiantes son evaluados con exámenes únicos independientemente de quien imparta la materia. En este contexto, para alcanzar colectivamente las metas educativas resultan insuficientes los esfuerzos que podemos realizar en el cómo enseñar. La elaboración de programas que permiten amplias y diversas interpretaciones, también resulta insuficiente. Para conseguir la homogeneización y lograr una articulación en la comunicación es indispensable contar, colectivamente, con técnicas y materiales que perfilen -con la menor dispersión posible- el qué enseñar. En otras palabras, es necesario delimitar con precisión las metas educativas, que se pretenden alcanzar en los cursos. Como un primer paso hacia el objetivo anterior, nos inclinamos a emplear algunas técnicas educativas existentes para la elaboración de programas, los cuales hemos denominado programas tecnificados o guías tecnificadas. El objetivo del elemento que estamos presentando consiste, entonces, en incidir en la elaboración de programas de grupos; un punto óptimo en esta esfera lo constituiría el contar con las metas que se persiguen en ciertas colecciones de objetivos; el desglose de los objetivos mismos; ejemplos o ejercicios que señalen los conceptos elementales que se deberán denominar para poder integrar la meta educativa; ejemplos de autoevaluación, y la clasificación taxonómica de cada objetivo con el fin de establecer una advertencia o sugerencia respecto al cuidado o dedicación que debe ponerse en el proceso de instrucción asociado. Esta labor descubre, a veces, la necesidad de presentar conceptos y temas cuya incorporación y nivel de profundidad no habían sido siquiera imaginados; esto es evidentemente importante durante el diseño e investigación curricular. Con fundamento en las ideas esbozadas en este punto decidimos elaborar una guía tecnificada sobre un curso de ecuaciones diferenciales, y de esta labor resultaron dos propuestas: una centraba el curso en la idea de operadores (ver el desarrollo del punto 3); la otra contemplaba todos los conceptos que aparecen en el programa vigente. Ambas guías tecnificadas seguían las ideas ya expuestas; a saber: establecimiento de las metas y submetas del curso; especificación de los objetivos que componen cada submeta; la clasificación taxonómica y la autoevaluación (ver el punto 4). Después de afinar estas guías tecnificadas para dos cursos de ecuaciones diferenciales, emprendimos la experiencia-aprendizaje de una de ellas, específicamente la que contiene la versión de operadores, en el Sistema de Aprendizaje Individualizado (SAI) de la UAM-A. Los índices de aprobados arrojaron las siguientes cantidades: (7)
(7) En estas cantidades no se contempla el índice de deserción de alumnos. Una vez más es necesario aclarar que no pretendemos obtener conclusión definitiva alguna con base en las cifras anteriores; pero sí queremos asentar que los resultados sobre este punto nos dan una perspectiva optimista. Antes de finalizar la exposición de este punto, queremos dejar constancia de parte de la información que obtuvimos de las evaluaciones que realizamos durante los dos semestres, en que experimentamos el material de ecuaciones diferenciales en el SAI.
Con base en esta información, surgió la necesidad de modificar la redacción y presentación de la unidad que presentaba ambigüedad en las metas y objetivos. Esto a su vez nos llevó a incluir un tema no contemplado en el plan o programa de estudio. Respecto a las unidades de aplicación, las presentamos de tal manera que responde al nuevo contexto que exige un conocimiento más sustancial del terreno de la aplicación. Una vez bosquejados por separado los elementos que componen nuestro esquema de trabajo, es indispensable observar lo siguiente: La naturaleza de cada uno de los elementos es profundamente interactiva con la de los restantes; así, por ejemplo, tener claras y desglosadas las metas educativas es insuficiente para los fines del desarrollo curricular, a menos que conozcamos el empleo y especificidad del conocimiento. También, resulta restrictivo cualquier diseño curricular ajeno al historial de los alumnos, y así sucesivamente. Aunque los elementos mostrados con anterioridad pudiesen dar la apariencia de estar completos, de hecho son todavía insuficientes para el diseño curricular. Basta recordar que no se contemplan los elementos derivados de las siguientes perspectivas: las exigencias curriculares de la planta productiva del país y las provenientes de considerar a la matemática como parte integrante e insoslayable de la cultura a la cual tiene derecho cualquier ciudadano.(8) (8) Véase nota 3 de la Bibliografía. Es claro que una vez perfilado un currículum con base en los elementos anteriores, se podrá pasar al establecimiento de propuestas de programas para cursos específicos. Señalemos, sin embargo, que ambas miras -currículum y programas- se entretejen a lo largo de nuestra labor y hoy por hoy sólo mediante esfuerzos logramos ver de manera separada ambos conceptos.(9) (9) Véanse notas 4 y 7 de la Bibliografía. Si bien los seis elementos presentados forman parte de nuestras herramientas para elaborar y diseñar cursos. no por este hecho los ubicamos como parte obligada en la reflexión curricular. Nosotros preferimos cobijar estos elementos bajo el nombre de desarrollo curricular y reservar el de investigación curricular para aquella actividad cuyo interés primordial es el sustrato, el sedimento, obtenido de la práctica y que exige ser analizado para ubicar sus conceptos básicos y las leyes que los rigen. Por ejemplo, podemos emplear el resultado de ciertas evaluaciones para decidir sobre la corrección de determinadas metas educativas, su relación y jerarquía, o bien examinar la posibilidad de presentar determinadas metas bajo una óptica diferente; cuando realizamos estas labores, empleamos el nombre de investigación curricular. Ahora bien, cuando empleamos las mismas evaluaciones para mejorar índices de aprovechamiento, elaborar material de reforzamiento, etcétera, aquí decidimos que estamos laborando en desarrollo curricular. 1. ARAGON, G. et al. Sobre programas tecnificados de ecuaciones diferenciales. Reporte de investigación Nº 30, de la División de Ciencias Básicas e Ingeniería. UAM. 2. ARAGON, G. et al. Reporte de investigación Nº 31 de la División de Ciencias Básicas e Ingeniería. UAM. Este reporte contiene:
3. CASTREJON DIEZ, J. et al. Planeación y modelos universitarios. Volumen I. México: ANUIES, 1975. (Ver Capítulo 4.) 4. GRAYSON, LAWRENCE P. La elaboración de los planes de estudio de ingeniería. UNESCO. Estudios sobre la formación de ingenieros, 5. 5. HAWSON, A. G. Análisis crítico del desarrollo curricular en educación matemática, en: Nuevas tendencias en la enseñanza de la matemática. Vol. IV. UNESCO, 1979. 6. MORRIS, KLINE. El fracaso de la matemática moderna. Ed. Siglo XXI. 7. JOHNSON JR., MAURITZ. La teoría del currículum (definiciones y modelos). Educational theory. Vol. 17, Nº 2, abril, 1967. 8. Nuevas tendencias en la enseñanza de las matemáticas. Vol. III. UNESCO, 1973. Ver en particular los capítulos 8 y 10 y las referencias citadas al final de los mismos. |
|||||||||||||||||||||||||||||