OBJETIVO Contenido El objetivo de este trabajo es indicar algunos aspectos que conviene reforzar en el uso de la matemática elemental y en el uso del español, considerando el empleo que les dan profesionales de diversas disciplinas. Estas indicaciones, extraídas de la experiencia, permitirán a las autoridades educativas diseñar objetivos, políticas y planes de estudio para los distintos niveles educativos, más acordes con la realidad del país y coherentes entre sí y, por otra parte, disponer de alternativas en el establecimiento de políticas, procedimientos y temática de los programas de educación continua en el nivel postuniversitario. Antecedentes Contenido Las consideraciones a que se refiere este trabajo son observaciones obtenidas, durante varios años, de impartir cursos de actualización profesional, en diversos centros de trabajo, a egresados de los planteles de educación superior de casi todo el país. Por así decirlo, estos profesionales forman un grupo selecto, en el sentido de que procuran mantenerse al día por medio de revistas técnicas y de cursos de actualización. Lo anterior es importante puesto que, en general, existe la creencia de que, al egresar de una carrera, se es profesional fuera del tiempo y del espacio, por lo tanto, no hay necesidad de continuar el propio desarrollo. Los temas tratados en los cursos pertenecen al campo de la matemática y se indican en la Tabla 1, atendiendo al número de veces que se han impartido. Como se ve en la tabla, la estadística es el curso más solicitado; el control de calidad, la optimización, la bioestadística y la computación juntos despiertan tanto interés como ella; asimismo, el diseño de experimentos, el muestreo y la investigación de operaciones comienzan a interesar a los profesionales. Debido a la utilidad que representa para la autoridad educativa, identificar las ramas de la matemática que tienen demanda en la actualización profesional, se elaboró la Tabla 2, que indica la rama de la matemática y los profesionales que han solicitado y atendido cursos de actualización en ella. Esta tabla permite agrupar a los profesionales atendiendo a su conocimiento y dominio de la matemática i) el matemático-físico-ingeniero, ii) el químico y iii) el médico-biólogo-arqueólogo-administrador. Por supuesto que estos grupos no son homogéneos. Desarrollo y resultados Contenido Los cursos de actualización profesional se caracterizan por reunir personal de diferentes disciplinas y de distintas generaciones, lo que da lugar a la formación de grupos heterogéneos en conocimientos matemáticos (ver Tabla 2). 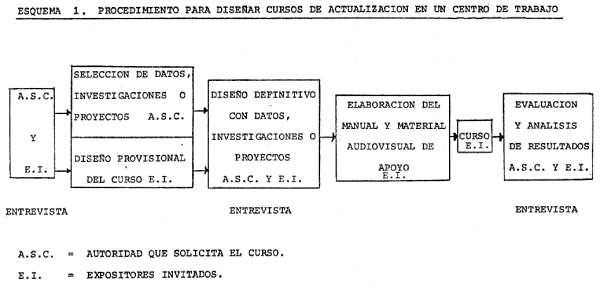Debido a esta heterogeneidad y considerando la transmisión y habilitación de conocimientos, así como el control para evaluar ambos aspectos, se generó un procedimiento para el diseño de este tipo de cursos (ver Esquema 1) y un diseño del curso fundamentado en información básica (Tabla 3). Dado que el procedimiento puede ser una alternativa viable en este tipo de actividades, se señalan someramente detalles de él. El diseño de estos cursos supone ciertos hechos (extraídos de la experiencia) que se plantean en forma de postulados y que se enumeran a continuación: Postulado 1. El educando, poco o nada de tiempo le dedica al aprendizaje del curso, fuera del horario de clases. Postulado 2. La autoridad está dispuesta a establecer políticas de estímulos para mantener actualizado a su personal. El Esquema 1 exhibe una interacción directa entre las autori- dades y los expositores que permite elegir los temas y el nivel al que conviene impartirlos, así como evaluar y analizar los resultados del curso. La elaboración del manual de apoyo es importante puesto que permite al educando concentrarse en la comprensión del material más que en su registro (toma de notas), incluir conceptos y ejercicios aclaratorios y de habilitación que hacen posible la discusión del material, la ilustración de temas y simplificación de procedimientos por medio de formatos y algoritmos, ad hoc. Por lo anterior es necesario destinar tiempo suficiente para elaborar el manual del curso (referencias 1, 2 y 3) y también para conseguir algún otro material de apoyo como libros, artículos, normas técnicas, nomogramas, etc., aparte de considerar el hecho de que los expositores son investigadores que desarrollan sus propios proyectos o estudios y que los más, imparten tres cursos de actualización al año. Los datos de la Tabla 3 permiten, entre otras consideraciones, orientar el curso, determinar su duración e intensidad (por lo general los cursos son cortos pero intensos, su duración es de una o dos semanas y requieren de un tiempo mínimo de tres y uno máximo de siete horas diarias). Estos cursos se imparten por dos expositores profundamente compenetrados de los fines y medios para capacitar a los educandos. El número de asistentes es de 10 a 25. La política de estímulos, la participación de la autoridad y la "carga de trabajo" del asistente son datos capitales para el buen término del evento. Es notable que las mejores respuestas a estos cursos hayan sido las que se han realizado con una política de estímulos muy eficiente, en las que la autoridad ha participado directamente en la actualización y en las que las horas destinadas a ejercicios se han aprovechado integramente. Otros resultados relevantes son: 1. El curso es objetivo, preciso y serio (cada educando dispone de un temario, que se cumple integramente, y un manual de apoyo). 2. Logra la participación de la autoridad, hecho muy estimulante para el profesional. 3. Detecta el nivel de comprensión, la actitud y la habilidad de cada educando por medio de la asesoría personal de los expositores. 4. Ayuda al profesional, individualmente, a superar sus limitaciones. Precisamente por haber podido observar las limitaciones individuales y de grupo de cada educando, es posible señalar hábitos y actitudes tan alarmantes como la "falta de orden lógico" para desarrollar un trabajo, la falta de responsabilidad individual, la falta de colaboración en trabajos de grupo y la persistencia de un pensamiento determinista (ver Tabla 4). Para evitar las "malformaciones" que producen estos hábitos y actitudes se deben erradicar desde la primaria y cuidar que no aparezcan en ninguno de los niveles educativos posteriores. Sobre el empleo que se le da a la matemática se señalan aspectos generales como la confusión de conceptos, la falta de conocimientos y de información básica, así como la omisión de símbolos (ver Tabla 5). En particular es notable la existencia de dificultades en el manejo del símbolo decimal, los quebrados y las fórmulas con diferente notación (ver Tabla 6). O bien, el desconocimiento y aplicación de las propiedades de orden de los números reales, los números primos y el uso de diversos índices, subíndices y tablas (ver Tabla 7). La falta de habilidad para plantear problemas e hipótesis de trabajo o ejecutar ordenadamente una tarea (ver Tabla 8). La omisión de símbolos como los identificadores, el punto decimal, los paréntesis e igualdades (ver Tabla 9). El establecimiento de suposiciones falsas como que las ramas de la matemática están ordenadas en una sucesión finita que termina en el cálculo diferencial e integral de una o varias variables, en las ecuaciones diferenciales ordinarias o parciales o en las ecuaciones integrales, dependiendo de la carrera profesional que se haya estudiado; que los temas que han visto en sus respectivos cursos son los únicos que trata esa rama, etc. (ver Tabla 10). Por otra parte, puesto que el desarrollo de la matemática se expresa en el idioma español, su enseñanza permite observar los empleos que se le dan a este idioma. Por ejemplo, existe una deficiencia en la comprensión en la "lectura en silencio y en "voz alta, hay desconocimiento de reglas gramaticales, mala ortografía, imprecisión y empobrecimiento del lenguaje (ver la Tabla 11). Las tablas -de la 6 a la 10- son particularmente importantes pues marcan limitaciones que no se pueden pasar por alto y su existencia es un indicador de la falla del sistema educativo. Además, por la falta de canales idóneos y permanentes entre el sistema educativo y la vida profesional, se nota que hay conceptos y material que no se incluyen en los programas convencionales ni se difunden por otro medio, a pesar del papel trascendente que ocupan en la tecnología moderna (referencia 4). Entre los conocimientos que es necesario impartir se encuentran: 1) los distintos sistemas numéricos (uno de los cuales es el sistema decimal) indicando las facilidades que ofrecen para la representación, operación y nemotecnia de los números; 2) el método científico y su aplicación en el desarrollo de protocolos de investigación; 3) el sistema internacional de unidades (SI), versión moderna del sistema métrico decimal; 4) las diversas máquinas de cálculo numérico desde el ábaco (que en México se ve como juguete desperdiciándose su imagen concreta para representar y efectuar operaciones), hasta las calculadoras de bolsillo y las grandes computadoras electrónicas; 5) la elaboración de definiciones, de tablas y gráficas que son elementos tan importantes en la actividad profesional, de los cuales se debiera insistir en su práctica en todas las etapas educativas; 6) señalar las numerosas ramas de la matemática. Como se puede ver, la mayoría de las limitaciones pertenecen a conocimientos fundamentales, tanto en lo que se refiere a la matemática y al español como al de hábitos y actitudes. 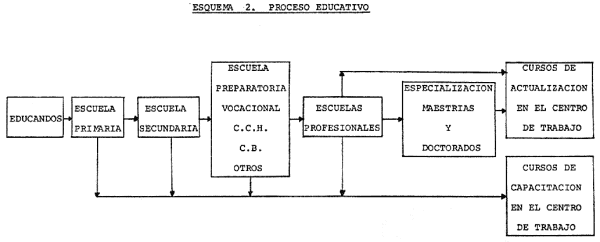En el Esquema 2 se presenta, gráficamente, la red que conforma el sistema educativo de que dispone el país. En él aparecen los niveles educativos a que se refiere este artículo, quizás una novedad de él sea la incorporación de la capacitación y actualización en los centros de trabajo y la ubicación de los especialistas y postgraduados dentro del sistema laboral. Las observaciones señaladas corresponden a los egresados de las últimas etapas del sistema educativo, que sin embargo muestran deficiencias notables en su formación básica. Por lo tanto, es necesario reconsiderar la finalidad del sistema educativo para así determinar, adecuadamente, el planteamiento de objetivos y de procedimientos que se deben seguir en cada uno de los niveles educativos, pensándolos como un sistema coherente tal, que permita eliminar las deficiencias exhibidas y capacitar sólidamente a los estudiantes eliminando así la cadena de consecuencias que llega hasta el profesional, elemento clave de la productividad del país. Por último, un hecho que subraya este traba jo es la demanda creciente de capacitación matemática por parte de disciplinas tradicionalmente ajenas a ella pero que, en la actualidad, necesitan de su conocimiento y dominio para continuar el desarrollo de su actividad profesional (médicos, biólogos, arqueólogos y administradores). Conclusiones Contenido 1. Hay hábitos y actitudes mentales que impiden a los profesionales desarrollarse plenamente (sobre todo la falta de orden y de responsabilidad individual). Estos hábitos se pueden modificar al considerarlos en los objetivos, políticas y planes de estudio de cada una de las etapas del sistema educativo. 2. Casi todas las disciplinas profesionales usan, en la actualidad, alguna rama de la matemática. Por lo tanto, hay profesionales de estas disciplinas que desean capacitarse en ella, pero se enfrentan a la formidable tarea de rebasar sus limitaciones en el uso de la matemática elemental. 3. La mayoría de las deficiencias matemáticas señaladas corresponden a conocimientos elementales. 4. Los profesionales con disciplinas tradicionalmente consideradas ajenas a la matemática, muestran limitaciones más marcadas en el uso de conocimientos de la matemática elemental que cursaron obligatoriamente. 5. Existe una falta de información sobre los temas matemáticos de interés general que no están incluidos en los temarios convencionales ni se imparten por ningún otro medio. 6. Hay deficiencias en el uso del idioma español que pueden corregirse en las etapas iniciales, y debe fomentarse, durante todas las etapas del sistema educativo, el gusto por hablar y escribir con propiedad, lo cual elevará el nivel cultural del universitario. 7. Tanto el procedimiento para diseñar cursos en el centro de trabajo como el diseño del curso son alternativas para establecer objetivos, políticas y temarios de los programas de educación continua. 8. Una forma de estimular la actitud mental adecuada para que el profesional se mantenga al día es establecer una eficiente política de estímulos. Por similitud, para mejorar el sistema educativo actual es necesario establecer y llevar a cabo una eficiente política de estímulos a los profesores. 9. La participación de las autoridades durante los cursos de actualización profesional es estimulante para el educando de este nivel. 10. Los ejercicios del curso que utilizan datos, planteamientos o problemas típicos del centro de trabajo mantienen vivo el interés del educando. Recomendaciones Contenido 1. Reforzar el aprendizaje de los puntos señalados en hábitos y actitudes mentales de los profesionales, como en los indicados en deficiencias matemáticas, debido a su propio carácter constructivo y a la demanda creciente de técnicas matemáticas en todas las áreas de la productividad. 2. Destinar en los cursos de matemáticas una sección que se puede considerar como "un laboratorio de matemáticas, que utilice ejercicios extraídos de la vida real del educando, cuyo planteamiento demande la asignación de tareas individuales que, juntas, integren un trabajo de grupo; es conveniente que las tareas se realicen con base en un protocolo de investigación elaborado por los propios estudiantes. 3. Generar políticas de estímulos para los profesores, con el fin de que ellos desempeñen, creativamente, su labor fundamental. Estos estímulos pueden incluir: i) becas para participar como asistente, ponente, etc., en congresos, simposia, seminarios, conferencias, tanto nacionales como internacionales, ii) becas para asistir a cursos de actualización, nacionales e internacionales, iii) establecer premios, en dinero, en lotes de libros, en inscripciones a revistas técnicas, en aumento de días económicos, en material educativo, en publicaciones de ensayos, investigaciones o experiencias educativas, etc. 4. Establecer ciclos de conferencias de divulgación (para maestros y alumnos) invitando a matemáticos y a profesionales que aplican la matemática en su trabajo diario. Estos ciclos pueden ser de periodicidad diversa y con determinados temas para que los asistentes elaboren composiciones, reportes, esquemas, gráficas, dibujos, etc., estimulándose tanto el aspecto matemático como el del lenguaje. 5. Implantar concursos de matemáticas que pueden ser: i) Sobre conocimientos a distintos niveles. ii) Sobre elaboración de material de apoyo como libros manuales, dispositivos educativos, juguetes, etc. iii) Sobre uso de material tecnológico actual que facilite y apoye el aprendizaje de la matemática. iv) Sobre la matemática entre los antiguos mexicanos, los mayas y los distintos grupos étnicos que integran el país. v) Sobre los matemáticos sobresalientes en México y en otros países. 6. Instrumentar programas de visita guiadas a centros de trabajo donde colaboran matemáticos y profesionales que aplican la matemática en su trabajo diario. Tabla 1 Contenido TEMAS DE CURSOS DE ACTUALIZACION PROFESIONAL   Tema N° de veces 1. Introducción a la estadística matemática 9 2. Control estadístico de calidad 4 3. Optimización de procesos 3 4. Bioestadística 2 5. Computación 2 6. Diseño de experimentos 1 7. Muestreo estadístico 1 8. Investigación de operaciones 1 Tabla 2 Contenido RAMA DE LA MATEMATICA Y PROFESIONALES QUE HAN SOLICITADO Y ATENDIDO CURSOS DE CAPACITACION EN ELLA Rama matemática Profesional Estadística matemática (*) y computación Matemático Químico Físico Biólogo Arqueólogo Administrador Ing. químico Ing. petrolero Ing. mecánico Ing. civil Ing. en informática Bioestadística (*) y muestreo(*) Biólogo (bacteriólogo y genetista) Médico (General y con especialidad en): Cardiología Pediatría Radiología Ortopedia Gastroenterología Ginecología Epidermis Control estadístico de calidad(*), optimización e investigación de operaciones Químico Ing. químico Ing. petrolero Administrador Diseño de experimentos (*) Biólogo (bacteriólogo y genetista) Químico Ing. químico Ing. petrolero (*)La probabilidad está considerada, implícitamente, en la presentación del tema. Tabla 3 Contenido DISEÑO DEL CURSO 1. Orientación del curso 2. Diseño del temario 3. Duración, intensidad y cupo del curso 4. Participación de la autoridad 5. Capacitación del personal 6. Material de apoyo del educando 7. Equipo de apoyo del curso 8. Expositores Información básica para el diseño A. a) Finalidad del curso b) Utilidad que se le piensa dar c) Actividades de que es responsable el centro de trabajo d) Problemas matemáticos que se han presentado e) Tipo de datos que manejan f) Facilidades de cómputo g) Nivel de conocimientos matemáticos de los profesionales que asistirán al curso y especialidad h) Número de asistentes i) Políticas de estímulo de la empresa B. Disponibilidad de los educandos, considerando la "carga" y responsabilidad de trabajo que soportan dentro de la empresa Tabla 4 Contenido HABITOS Y ACTITUDES MENTALES 1. No tienen el hábito de seguir un orden "lógico" para desarrollar un trabajo 2. Tienen el hábito de copiar 3. Rechazan responsabilizarse de lo que afirman verbalmente o por escrito. Usan expresiones como: "eso dije", "eso iba a decir", "es lo que estaba pensando", "exactamente", etc. 4. Rechazan responsabilizarse, individualmente, de una tarea. Dicen preferir realizar trabajo de equipo pero, en la práctica, el grupo se beneficia del trabajo de una o dos personas 5. Sistemáticamente, muestran un pensamiento determinista. Les cuesta trabajo comprender la probabilidad de ocurrencia de un hecho, una afirmación o una hipótesis. Inclusive, en el caso de los procesos de medición (que son propios de las disciplinas experimentales), les resulta difícil asociar los planteamientos necesarios para efectuar una inferencia estadística de la muestra a la población. Tabla 5 Contenido ASPECTOS DE QUE ADOLECEN PROFESIONALES DE DIVERSAS DISCIPLINAS EN EL USO DE LA MATEMATICA 1. Confusión de conceptos 2. Desconocimiento de conceptos y métodos u otros conocimientos 3. Omisión de símbolos matemáticos 4. Falta de habilidad 5. Establecimiento de suposiciones falsas Tabla 6 Contenido CONFUSION DE CONCEPTOS 1. Al operar con el símbolo decimal 2. Al operar con quebrados 3. Al aplicar las reglas de redondeo de números 4. Al determinar el número de dígitos significativos 5. Al usar los números e y II 6. Al usar fórmulas con diferente notación Tabla 7 Contenido DESCONOCIMIENTO DE CONCEPTOS, METODOS U OTROS CONOCIMIENTOS 1. Propiedades de orden de los números reales 2. Números primos 3. Uso de las tablas de raíces cuadradas, logaritmos, etc 4. Uso de índices 5. Sucesiones numéricas 6. Factoriales 7. Combinaciones 8. Permutaciones 9. Funciones elementales 10. Sistemas numéricos como el binario, octal, sexagesimal, etc. 11. Método científico 12. Protocolos 13. Normas técnicas 14. Máquinas de calcular como: ábaco, regla de cálculo computadoras mecánicas y electrónicas y calculadoras de bolsillo Tabla 8 Contenido COMISION DE SIMBOLOS MATEMATICOS 1. Omisión del símbolo igual (=) al indicar la igualdad de dos cantidades, expresiones algebraicas, etc. 2. Omisión de símbolos como "implica que", o "equivalente A", al desarrollar una expresión algebraica. Por ejemplo, x + 2 = 5 --> x = 5 - 2 .¨. x = 3, lo escriben x + 2 = 5 = 5 - 2 = 3 3. Omisión de paréntesis al escribir una expresión. Por ejemplo: 2 + (-1) + (-8) + 15 + (-41), lo escriben como : 2 + - 1 - 8 + 15 + - 41 4. Omisión del punto decimal al escribir un número 5. Omisión de identificadores para los valores de una variable o de una cantidad. Por ejemplo, x = 0.151, lo han escrito como: 151. 6. Omisión del signo de un número Tabla 9 Contenido FALTA DE HABILIDAD 1. En el planteamiento de problemas 2. En el planteamiento de hipótesis de trabajo 3. En la ejecución ordenada de un trabajo 4. En el uso de fórmulas con distinta notación 5. En el uso de tablas 6. En el uso de índices 7. En la clasificación de números en intervalos particulares, usando relaciones de orden 8. En la construcción de definiciones 9. En lo construcción de tablas y gráficas 10. En el uso de nomogramas 11. En la interpretación de tablas, funciones y nomogramas, etc. 12. En generar otras aplicaciones Tabla 10 Contenido ESTABLECIMIENTO DE SUPOSICIONES FALSAS 1. Suponen que las ramas de la matemática están ordenadas en una sucesión como aritmética, geometría, álgebra ele- mental, trigonometría, geometría analítica, cálculo diferencial e integral de una variable, cálculo diferencial e integral de varias variables, ecuaciones diferenciales ordinarias, ecuaciones diferenciales parciales, ecuaciones integrales. 2. Suponen que, en general, después del cálculo diferencial e integral ya no hay otra rama de la matemática. 3. Suponen que los temas que, fortuitamente, han formado parte de sus cursos son los únicos que trata esa rama. 4. Suponen que no hay problemas sin resolver en las ramas mencionadas, en otras palabras, estas ramas están totalmente terminadas. Tabla 11 Contenido DEFICIENCIAS EN EL USO DE NUESTRO LENGUAJE 1. Comprensión deficiente en la lectura "en voz alta" o en "silencio". 2. Empobrecimiento del lenguaje. Incluso en una materia tan precisa como la matemática, usando como adjetivo expre- siones tan vagas como "está padre", "está bien esta onda", etcétera. 3. Desconocimiento de reglas de construcción gramatical. 4. Mala ortografía. 5. Separación de una palabra sin atender a las sílabas que la conforman o usando algún otro criterio que sea pertinente. BIBLIOGRAFIA Contenido 1. Cortés I., M. E. y G. F. P. Ramírez Introducción a la investigación de operaciones, publicado por el Instituto Mexicano del Petróleo, 1980. 2. Aut. Cit. Estadística aplicada a la inspección, publicado por el Instituto Mexicano del Petróleo, 1982. 3. Aut. Cit. Control estadístico de calidad, publicado por el Instituto Mexicano del Petróleo, 1981. 4. Aut. Cit.: "Sobre algunos aspectos de que adolecen los egresados de las carreras del área química en el manejo de datos", I Congreso Nacional de Educación Química, Cuernavaca, Mor., 1981. Contenido